Trembling Hands

At least since Selten (1975) game theorists have considered that given a series of decisions there is some small probability that the person making the decisions will make a mistake and do something irrational, even if she knows the right thing to do.  This is called the trembling hand approach: although a person rationally knows the right (rational) thing to do, sometimes her hand trembles and she chooses incorrectly.

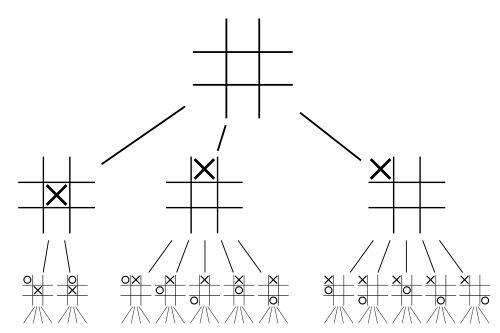
Therefore, given a game defined by a finite set of iterated decisions and payoffs in which all the rational moves are known by both players (think Tic Tac Toe), there is a ‘perturbed’ game in which the rational choices are not made.  So consider playing a game of Tic Tac Toe:  Either player can always force a draw in Tic Tac Toe and hence prevent loss.  However, it is easy enough to make a mistake (through inattentiveness, eg) and allow your opponent to win.

I believe this approach is a good start but does not go nearly far enough to incorporate probability into game theory.  The issue stems from the trembling hand approach assuming that irrational behavior occurs because of ‘some unspecified psychological mechanism.’  This is fine, but then every trembling hand probability, every chance of making an irrational decision, is defined as a separate, independent probability.  This means that making an irrational decision is based on chance, as if we roll a die every decision we make.

Perhaps some people have this problem, that they act irrationally at probabilistic rates, but this doesn’t seem either realistic, or fit with the idea that a psychological mechanism was at work.  If some psychological mechanism was at work, then we would expect

1. The probabilities of making mistakes would not be independent of each other, since they have a common source.
2. There would be a much higher chance of irrationality at times when the psychological issue manifests itself.

One example of what I have in mind is the effectiveness of gamesmanship in sport.  Gamesmanship is the art of getting into your opponents head and causing them to make mistakes.  Consider this description of “furbizia” in Italian soccer by Andrea Tallarita:

Perhaps nothing has been more influential in determining the popular perception of the Italian game than furbizia, the art of guile… The word ‘furbizia’ itself means guile, cunning or astuteness. It refers to a method which is often (and admittedly) rather sly, a not particularly by-the-book approach to the performative, tactical and psychological part of the game. Core to furbizia is that it is executed by means of stratagems which are available to all players on the pitch, not only to one team. What are these stratagems? Here are a few: tactical fouls, taking free kicks before the goalkeeper has finished positioning himself, time-wasting, physical or verbal provocation and all related psychological games, arguably even diving… Anyone can provoke an adversary, but it takes real guile (real furbizia) to find the weakest links in the other team’s psychology, then wear them out and bite them until something or someone gives in – all without ever breaking a single rule in the book of football. (via)

If we try to explain the an instance of someone making an irrational play in a game due to gamesmanship/furbizia according to the trembling hand model, we run into difficulty.  The decision tree according to the ‘trembling hand’ theory would have a series of decisions each with a low probability of making an irrational mistake:

.01 — .01 — .01 — .01 — .01
Hence it cannot explain why someone would crack later in the game as opposed to earlier, since all the probabilities are equal.  Nor can it explain why people make irrational decisions at higher rates when playing against a crafty opponent than they would make otherwise. Therefore the trembling hand model cannot explain the effectiveness of gamesmanship.

But the decision tree given linked, non-independent probabilities might have the chance of an irrational decision given by:

.01 — .05 — .1 — .17 — .25
This model has an increasing chance of irrational action.  As time progresses, it becomes increasingly likely that an irrational choice will occur due to the gamesmanship of the opponent.

I’ll refer to this model generally as induced irrationality.  Induced irrationality occurs when the chance of making a rational decision decreases due to some factor, or when the chances of making irrational decisions over time change in concert, or both.

Other phenomena follow this pattern.  Bullying comes to mind: it is similar to gamesmanship in its breaking or bending of ‘rules’ over time to get in someone’s head and thence get them to do things they would rather not do.  The bullied will act irrationally in the presence of the bully and potentially more so as the bullying continues, perhaps even leading to “snapping”— doing something seriously irrational.

Phobias are also similar: for whatever reason a person has a phobia, and given the presence of that object or situation, the otherwise rational person will make different decisions.

Moreover this may have something to do with the Gambler’s Fallacy:   By making a gambler associate a pattern to some random act, such as by showing the gambler all the recent values of a roulette wheel in order to convince the gambler to believe that the wheel likely will land on red (or losing a few bets to a shill in 3 card monte, or seeing a pattern in the stock market, etc.), the casino has planted a belief in the gambler.  Hence, as time goes on and red is not landed upon, the gambler increasingly thinks it is ever more likely that red will hit (even though it has the same low chance as it always did). Hence the gambler will likely bet more later — more irrationally —  as he expects red to be increasingly likely to hit.

Hence, though trembling hands may be a factor in irrational decision making, it does not seem like it is the only possibility or even the most significant in a number of interesting cases.

—————————————

Selten, R. (1975). ‘Re-examination of the Perfectness Concept for Equilibrium Points in Extensive Games.’ International Journal of Game Theory, 4: 22–55.

–

My brother beat the Tic Tac Toe playing chicken when the Chinatown Fair Arcade (NYC) still operated.  I assume that there was a computer choosing the game moves and it happened to glitch when my brother was playing: though the machine claimed it won, if you looked at the Xs and Os, my brother had won.  We asked the manager for our promised bag of fortune cookies.  He said he didn’t actually have a bag since the chicken wasn’t ever supposed to lose.